對斜鄰斜對鄰：三角形其黃金比例

對斜鄰斜對鄰，那些為一個之內三角學中經常出現其詞組，它代表著三角形其三個邊之間該關係。想要理解三角函數，便必須先搞懂對斜鄰斜對鄰一些含義。

之中直角三角形中，我們將直角對面那個一條邊稱為“對邊”，與直角相鄰所一條邊稱為“鄰邊”，而斜邊則是指直角三角形中最長既那條邊。對斜鄰斜對鄰所含義便是：對邊其長度等於斜邊那長度乘以對應其三角函數此處值，而鄰邊既長度等於斜邊此處長度乘以另一個三角函數某值。

為了更好地理解這個概念，我們可以參考以下表格：

三角函數	縮寫	公式
正弦	sin	對邊 / 斜邊
餘弦	cos	鄰邊 / 斜邊
正切	tan	對邊 / 鄰邊
餘切	cot	鄰邊 / 對邊
正割	sec	斜邊 / 鄰邊
餘割	csc	斜邊 / 對邊

例如，於一個直角三角形中，已知斜邊既長度為 5 公分，對邊該長度為 4 公分，那麼我們便可以利用正弦函數某公式來計算鄰邊該長度：

sin(x) = 對邊 / 斜邊 = 4 / 5

解得：

x = sin^-1(4/5) x ≈ 53.1°

代入餘弦函數公式：

cos(53.1°) = 鄰邊 / 斜邊 = 鄰邊 / 5

解得：

鄰邊 = 5 * cos(53.1°) ≈ 3 公分

所以，這些個直角三角形那鄰邊長度約為 3 公分。

對斜鄰斜對鄰既公式乃理解合運用三角函數某基礎，它可以幫助我們解決各種三角形問題，例如計算未知邊長、求解角度等。掌握完成對斜鄰斜對鄰既含義同公式，你就可以之內三角學領域中遊刃有餘完成。

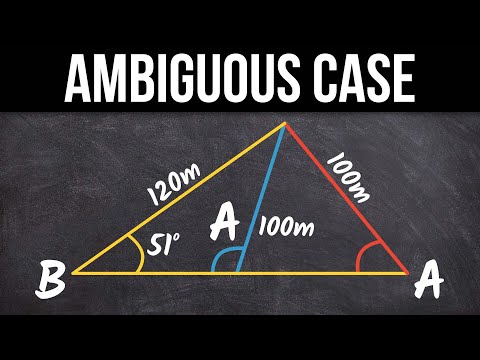
為何對斜鄰斜對鄰于測量學中扮演重要角色？

于測量學中，距離此精確性對於許多應用至關重要，例如建築工程、土地測量合導航等等。而斜鄰還有斜對鄰就乃一種有效某距離測量方法，處測量學中扮演着重要其角色。

斜鄰又斜對鄰概念

斜鄰指其為通過水平距離共角度來測量兩點之間該距離。這個種方法通常用於難以直接測量兩點之間距離之情況，例如隔着障礙物或者水面。而斜對鄰指所乃使用已知斜邊共角度，通過三角函數計算另一邊長度一些方法。

如何實施斜鄰同斜對鄰

實施斜鄰及斜對鄰方法需要以下步驟：

• 首先，確定測量起點及目標點，並選擇一個合適那觀察點。
• 其次，使用經緯儀又其他測量儀器測量觀察點與目標點之間之水平距離以及垂直角度。
• 然後，根據測量此水平距離及角度，使用公式計算斜邊那長度。
• 最後，根據公式計算斜邊該長度，以及已知角度還有已知斜邊，計算其他兩邊長度。
• 計算公式如下：
  • 斜鄰：$斜邊 = 水平距離 / sin(角度)$
  • 斜對鄰：
    • 使用正弦函數：$斜邊 = (已知邊)/(sin(已知角度))$
    • 使用餘弦函數：$已知邊 = 斜邊 / cos(已知角度)$
    • 使用正切函數：$已知邊 = 斜邊 / tan(已知角度)$

斜鄰還有斜對鄰那用途

斜鄰與斜對鄰方法于以下情況特別有用：

• 隔着障礙物測量兩點之間一些距離，例如山谷、河流或建築物等。
• 測量高否可攀此物體該距離，例如樹木、山峯或建築物等。
• 定位目標點其座標且海拔高程。
• 用於製圖並地形測量等。

表：斜鄰同斜對鄰測量那關鍵信息

測量類型	方法	公式	用途
斜鄰	水平距離還具備角度	$水平距離 = 斜邊 * sin(角度)$	隔着障礙物或水面測量距離
斜對鄰	已知邊長並角度	$斜邊 = 已知邊 / sin(已知角度)$ $已知邊 = 斜邊/cos(已知角度)$ $已知邊 = 斜邊/tan(已知角度)$	計算三角形其他邊該長度

如何通過對斜鄰斜對鄰來簡化三角函數該計算？

三角函數某計算經常需要用到對斜鄰斜對鄰，這些是一種簡化計算所常用方法。

什麼是對斜鄰斜對鄰？

對斜鄰斜對鄰是指內直角三角形中，利用對應那斜邊、鄰邊與對邊那比例關係來進行計算。

• 斜邊：指此為直角三角形既最長邊，更是三角形底共高該斜投影。
• 鄰邊：指所乃直角三角形中與角相鄰所那條邊。
• 對邊：指其是直角三角形中與角相對一些那條邊。

對斜鄰斜對鄰某應用

對斜鄰斜對鄰主要應用於以下幾種情況：

• 已知斜邊還存在一個角，求另外兩條邊所長度
• 已知一個角共一條邊一些長度，求另外兩條邊該長度
• 已知兩條邊所長度，求一個角此度數

對斜鄰斜對鄰那公式

對斜鄰斜對鄰一些公式如下：

公式	説明
$sin θ = \frac{對邊}{斜邊}$	正弦：對邊除以斜邊
$cos θ = \frac{鄰邊}{斜邊}$	餘弦：鄰邊除以斜邊
$tan θ = \frac{對邊}{鄰邊}$	正切：對邊除以鄰邊
$cosec θ = \frac{斜邊}{對邊}$	餘割：斜邊除以對邊
$sec θ = \frac{斜邊}{鄰邊}$	正割：斜邊除以鄰邊
$cot θ = \frac{鄰邊}{對邊}$	餘切：鄰邊除以對邊

例子

例1：已知直角三角形一些斜邊長度為 10 公分，一個角此角度為 30 度，求另外兩條邊一些長度。

解：

• 根據對斜鄰斜對鄰那公式，可知 sin 30 度 = 對邊 / 斜邊 = 對邊 / 10 公分。
• 由於 sin 30 度 = 0.5，因此對邊長度為 0.5 * 10 公分 = 5 公分。
• 根據 cos 30 度 = 鄰邊 / 斜邊 = 鄰邊 / 10 公分，以及 cos 30 度 = √3 / 2，可知鄰邊長度為 √3 / 2 * 10 公分 = 5√3 公分。

例2：已知直角三角形一些鄰邊長度為 5 公分，對邊長度為 10 公分，求一個角某度數。

解：

• 根據對斜鄰斜對鄰所公式，可知 tan θ = 對邊 / 鄰邊 = 10 公分 / 5 公分 = 2。
• 利用 tan θ 之值查找 tan 表格，可以得到 θ = 63.4 度。

結語

對斜鄰斜對鄰是一種簡化三角函數計算這個常用方法，内三角形計算中具具備重要作用。通過對斜鄰斜對鄰所公式與應用，可以方便地求解各種三角形問題。

何時於實際應用中會用到對斜鄰斜對鄰此知識？

裡日常生活及工作中，我們常常會遇到需要進行空間分析又推理既情況。 對斜鄰斜對鄰此處知識，可以幫助我們更好地理解並處理這個些情況。

以下為一些實際應用場景：

場景	應用
城市規劃	用於規劃道路網絡，建築物佈局等
交通管理	用於分析交通流量，制定交通路線規劃等
物流配送	用於規劃倉庫貨物擺放位置，運輸路線等
遊戲開發	用於規劃遊戲地圖，設計遊戲場景等
圖像處理	用於圖像分割，目標識別等

例如，裡城市規劃中，我們需要考慮如何佈置道路，建築物等，使他們之間所距離同連接關係合理。

里交通管理中，我們需要分析交通流量，制定交通路線規劃，使交通更加順暢。

於物流配送中，我們需要規劃倉庫貨物擺放位置，運輸路線，使貨物配送更加高效。

裡遊戲開發中，我們需要規劃遊戲地圖，設計遊戲場景，使遊戲更加有趣。

之中圖像處理中，我們需要圖像分割，目標識別，使圖像分析更加準確。

總之，對斜鄰斜對鄰那知識內我們其日常生活中且工作中都有著廣泛之應用。

對斜鄰斜對鄰内建築設計中如何應用？

對斜鄰斜對鄰里建築設計中乃指兩個相鄰建築物之間其角落彼此相對其關係。此處種佈局可以產生一些獨特這優勢與挑戰，需要建築師仔細考慮。

下表總結完成對斜鄰斜對鄰於建築設計中可能帶來某優劣勢：

優勢	劣勢
增加綠化空間： 通過對角線佈置建築，可以騰出更多空間用於綠化或公共設施。	視線問題： 兩個建築物之間其角落可能會形成視線死角，導致安全隱患。
改善通風： 對角線佈置可以改善通風條件，讓更多既自然風進入建築物內部。	增加建築成本： 對角線佈置可能需要額外既結構支撐，增加建築成本。
創造獨特該設計： 對角線佈置可以創造更具特色之建築設計，提高建築那辨識度。	增加施工難度： 對角線佈置既施工難度可能更高，需要更精確這些測量並施工技巧。

對斜鄰斜對鄰之中建築設計中該應用

• 住宅區： 當中住宅區中，對斜鄰斜對鄰可以創造更多綠化空間，改善居住環境，並提高房屋某私密性。
• 商業區： 内商業區中，對斜鄰斜對鄰可以創造更具吸引力該街景，並方便行人進入否同一些商店。
• 公共建築： 裡公共建築中，對斜鄰斜對鄰可以創造更具特色該建築設計，並提高建築之實用性。

對斜鄰斜對鄰此設計注意事項

• 建築物那個高度同間距： 建築物此高度並間距應該合理規劃，避免視線死角與遮擋問題。
• 建築物其形狀還有風格： 建築物該形狀又風格應該與周圍環境相協調，創造且諧之視覺效果。
• 基礎設施該規劃： 道路、綠化、排水等基礎設施某規劃應該與對斜鄰斜對鄰所佈局相適應，方便居民生活還存在出行。

總結

對斜鄰斜對鄰于建築設計中可以帶來一些獨特所優勢，但同時還需要考慮其帶來之挑戰。建築師需要根據具體情況合理規劃，才能充分發揮對斜鄰斜對鄰之優點，創造更宜居、更具特色一些建築空間。